
It is reported the magnetic characterization of the Fe3Ga4 intermetallic compound synthesized by the MFNN technique.
Nanowires belong to a new class of quasi-unidimensional materials that have been attracting great interest due to their numerous potential applications, such as functional materials in biomedical sciences, electronics, optics, magnetic devices and energy storage. Among the several ways to produce nanowires, one can mention template-assisted fabrication, vapor-liquid-solid mechanism, molecular beam epitaxy and electrochemical nanolithography.
In particular, nanoporous alumina membranes have been widely used as templates for magnetic nanowire arrays produced by electrochemical deposition due the simplicity, versatility, efficiency and low cost implementation of this technique. However, the nanowires obtained by this way generally present poor crystallinity and are restricted to metallic alloys.
Recently, the novel metallic-flux nanonucleation (MFNN) technique has been developed to nucleate crystalline nanowires inside alumina membrane pores [1]. The nanoporous template presents advantages, such as an excellent pore size control over large areas (obtained by varying the oxidation conditions), as well as pores with large aspect. By using an alumina template during a metallic flux growth, the MFNN technique allows to confine the crystalline compounds into a quasi-1D shape. In addition to the high probability to obtain single crystal nanowires, this technique opens opportunities to fabricate novel intermetallic compounds in nanowire shape, besides the advantage of simultaneously obtaining both systems (bulk and nanowires).
K. O. Moura et al., [2] have reported the magnetic characterization of the $ \rm Fe_{3}Ga_{4}$ intermetallic compound synthesized by the MFNN technique in both bulk and nanowire forms. $ \rm Fe_{3}Ga_{4}$ presents a complex base-centered monoclinic structure. It has also been observed that the bulk compound exhibits a complicated magnetic behavior. At low magnetic fields, a ferromagnetic (FM) state develops below temperature $ \rm T_{1} = 50 K$, while at higher temperatures, antiferromagnetism (AFM) takes place before vanishing at a Néel temperature $ \rm T_{2}=390K$. This behavior has been explained by Moriya and Usami’s theory, which predicts coexistence of FM and AFM states in itinerant electron systems. On the other hand, Fe-Ga nanowires, with different composition from that studied in this work, have been fabricated by electrochemical deposition and have been investigated for potential use as sensing elements in a variety of microelectromechanical and nanoelectromechanical-based biomimetic devices. Therefore, it is very instructive to study the dimensionality effects on $ Fe_{3}Ga_{4}$ properties. To the best of our knowledge, no such studies about $ Fe_{3}Ga_{4}$ compound have not yet been reported in the literature.

Figure 1. Scanning electron microscopy (SEM) images of (a) an isolated naowire and (b) 2 nanowires
Structural Characterization
Scanning electron microscopy (SEM) was performed at the Brazilian Nanotechnology Laboratory (LNnano) in Campinas to verify the presence, dimensions and composition of the $ \rm Fe_{3}Ga_{4}$ nanowires. As shown in Fig.1(a) and (b), most of the observed isolated nanowires exhibit a diameter of ~250 nm and a length of ~25 μm, giving a length/diameter aspect ratio of around 100. Figure 1(b) displays a magnified view of two nanowires showing their surface quality by presenting a very low roughness and no apparent defects. X-Ray diffraction (XRD) data, performed with $\rm Cu K_{\alpha}$ radiation, were used to identify the bulk crystalline phase. However, the nanowires structural characterization required synchrotron X-Ray diffraction and absorption measurements, both performed at the Brazilian Synchrotron Light Laboratory (LNLS). The diffraction profile of the empty membrane could be reasonably well modeled by an admixture of $ \eta$- and $ \rm \theta-Al_{2}O_{3}$ phases, with no clear sign of contamination with impurity phases. However, in the treated membrane with nanowires, the cubic $ \rm \eta-Al_{2}O_{3}$ phase was not clearly observed. Instead, the results could be modeled by a mixture of two $ \rm \theta-Al_{2}O_{3}$ phases, leading to an inhomogeneous solid solution with an $ \rm Al_{1.4}Ga_{0.6}O_{3}$ majority phase and an $ \rm Al_{0.6}Ga_{1.4}O_{3}$ minority phase. Extra Bragg peaks due to additional polycrystalline phases were also observed in the membrane with embedded nanowires profile and they could not be related to any known phase of the Fe-Ga binary system, and most likely arise from additional phases of the $ \rm Al_{2-x}Ga_{x}O_{3}$ membrane.
In order to obtain structural information of the phases containing Fe, an element-specific technique became necessary. X-Ray absorption measurements were therefore performed at the Fe K-edge in fluorescence mode at the XAFS2 beamline (LNLS) on the embedded nanowires: they showed the presence of oxidized Fe3+ in the membrane with nanowires sample to a small degree of substitution of Fe atoms into the $ \rm Al_{2-x}Ga_{x}O_{3}$ membrane, while the major metallic Fe component found in the absorption spectrum is attributed to the $ \rm Fe_{3}Ga_{4}$ nanowires. Despite the good overall agreement provided by this simple analysis using $ \rm Fe_{2}O_{3}$ and $ \rm Fe_{3}Ga_{4}$ standards, a clear discrepancy between the observed spectrum for the embedded nanowires sample and the mixture of standards could be seen at ~7160 eV. This may be attributed to a distinct non-local electronic structure of $ \rm \alpha-Fe_{2}O_{3}$ with respect to $ \rm Fe_{3+}$ ions impurity into the $ \rm Al_{2-x}Ga_{x}O_{3}$ membrane, which may lead to large energy shifts of high-energy XANES excitations involving charge transfer from Fe to neighboring ions.
Magnetic Characterization
Magnetization measurements were done both as a function of temperature T (2–400 K) and applied magnetic field H (± 20 kOe). For the nanowire array characterization, the magnetic field was applied parallel to the nanowires axis. From the magnetization as a function of temperature curves, the two expected magnetic phase transitions are distinguished in terms of a magnetization drop around 50 K ($ \rm T_{1}$) and a peak around 390 K ($ \rm T_{2}$). In the case of nanowires, the reduced dimensionality affects $ \rm T_{1}$ and $ \rm T_{2}$ values in opposite ways. As we can see in Fig. 2, $ \rm T_{1}$ increases while $ \rm T_{2}$ decreases. Moreover, the relative magnetization drop at the first temperature transition $ \rm T_{1}$ is smaller for the nanowire array compared to the bulk one. This could suggest that one is dealing with a phase transition from a FM to another magnetic phase order with net macroscopic magnetization in the nanowire case (FERRI or coexistence of FM and AFM). As discussed later, this phase coexistence is predictable from Moriya’s theory. This is the first evidence that the nature of this transition differs in the nanowires and in the bulk samples. The temperature-dependent magnetization curves exhibit appreciable thermal hysteresis around $ \rm T_{1}$, but only in the $ \rm Fe_{3}Ga_{4}$ nanowires case, which decreases when we increase the applied magnetic field. These effects are characteristic of first order phase transition. In the case of bulk samples, no thermal hysteresis is noticed. Furthermore, we can see that the magnetic signal from $ \rm Fe_{3}Ga_{4}$ phase (in emu/g) is about 500 times smaller that for the bulk crystal, which is consistent with the estimative by XRD that the weight fraction of the $ \rm Fe_{3}Ga_{4}$ phase in the membrane is below 2%. Between 50 and 300 K, one observes a field-induced transition on the field-dependent magnetization curves for the bulk compound. On the other hand, no such transition is detected for the nanowire system, but rather a large magnetic susceptibility and the presence of a magnetic hysteresis between 2 and 300 K, also supporting the FERRI or coexistence FM and AFM behavior suggested before.
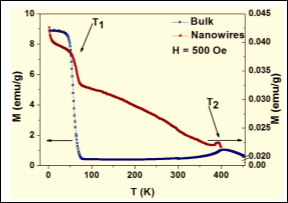
Figure 2. Temperature-dependent magnetization curves for Fe3Ga4 bulk (blue symbols, left axis) and nanowire array (red symbols, right axis) with an applied field of 500 Oe.
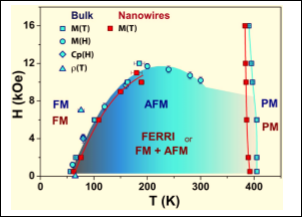
Figure 3. Magnetic phase diagram for Fe3Ga4 bulk and nanowires showing the effect on the transition temperatures due to the lower dimensionality.
Specific Heat Characterization
Specific heat (C) measurements were performed in the 2–100 K and 2–20 kOe ranges. The result shows that the nanowire exhibits the same crystalline structure than that of $ \rm Fe_{3}Ga_{4}$ bulk phase. Moreover, one observes a reduction in the contribution of the conduction electrons to the specific heat when the system dimensionality is reduced. Remarkably, the electronic coefficient (γ) drops from 25.60 $ \rm mJ/mol.K^{2}$ to almost zero, indicating that the $ \rm Fe_{3}Ga_{4}$ compound tends to become insulating in the nanowire. These data are consistent with the magnetization results, since that a FERRI or FM behavior is most likely to be expected in localized electron magnetism.
Electrical Characterization
Bulk electrical resistivity measurements were performed using a standard four-probe technique in the 2–400 K temperature range and under magnetic fields of 0 and 7 kOe. The results revealed that the resistivity of metamagnetic compounds is dominated by spin fluctuations, an important aspect that justifies the use of Moriya’s theory to explain the $ \rm Fe_{3}Ga_{4}$ compound magnetic behavior. With a magnetic field of 7 kOe, the temperature where the resistivity slope is changing, which happens to be 70 K, increases, in agreement with the magnetization results.
Magnetic Phase Diagram
Experimental magnetic, specific heat and electrical results yield to the built magnetic phase diagrams of the $ \rm Fe_{3}Ga_{4}$ bulk and for the system at low dimensionality (Fig. 3). Based on these observations and Moriya and Usami’s theory, there are strong evidences that the effects of reducing dimensionality can be explained as resulting from modifications of the system free energy. Those modifications originate from electronic structure changes, and end up affecting the compound magnetic phase diagram. Thus, $ \rm Fe_{3}Ga_{4}$ bulk compound would exhibit at $ \rm T_{1}$ either a ferromagnetic to antiferromagnetic transition (in agreement with the literature for bulk), or a ferromagnetic to ferrimagnetic or coexistence of ferromagnetic and antiferromagnetic transition, if under nanowire form. The specific heat data are also consistent with these conclusions, since a FERRI or FM behavior is most likely to be expected in localized electron magnetism. Finally, at $ \rm T_{2}$, the applied field decreases the temperature of maximum susceptibility similarly for both systems.
Sources:
[1] Pirota, K. R. et al. Processo de produção de nanofios monocristalinos intermetálicos. BR patent 10 2014 019794 0 issued 11 Aug. 2014.
[2] O. Moura, L. A. S. de Oliveira, P. F. S. Rosa, C. B. R. Jesus, M. E. Saleta, E. Granado, F. Béron, P. G. Pagliuso & K. R. Pirota. Dimensionality tuning of the electronic structure in Fe3Ga4 magnetic materials. Scientific Reports 6, Article number: 28364 (2016). doi:10.1038/srep28364
A detailed analysis highlights several structural complexities of the (BZCY72) perovskite.
The results demonstrate for the first time the antiviral activity of mSiO2 particles.